10. Molecular mechanics:

Molecule parameters like molecular geometry, heat of formation, strain energy, dipole moment, and vibrational frequencies can be calculated empirically using the molecular mechanics approach.

• Energy calculations in molecular modeling

• Optimization of molecular structure

• Conformational search

• Energy minimization

• Molecular dynamics

 

When it comes to Newtonian mechanics, molecules are viewed like objects.

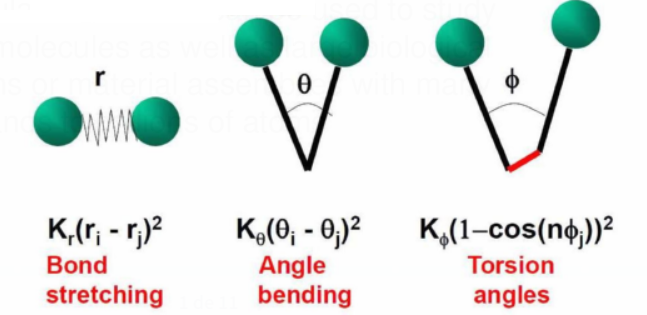
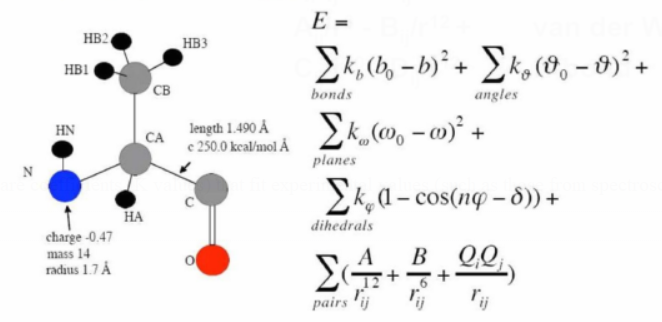
Energy Terms

Different energy words are used to account for bonded and non-bonded interactions.

The geometry of chemical bonds and dihedral angles are two examples of bonded interactions.

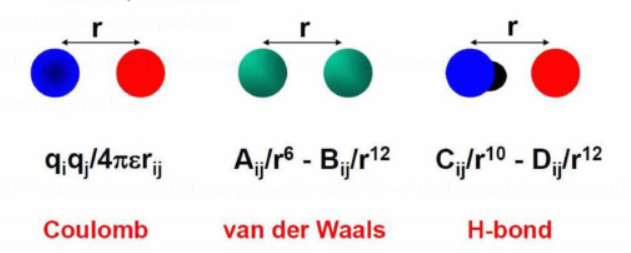
Van der Waals (vdW) interactions, electrostatic interactions, and hydrogen bonds are examples of non-bonded interactions.

Deviations from optimal (experimental) values are explained by Hook's law and other harmonic potentials.

 

 

Non-bonded interactions: Atomic spheres are assigned point charges for electrostatics.

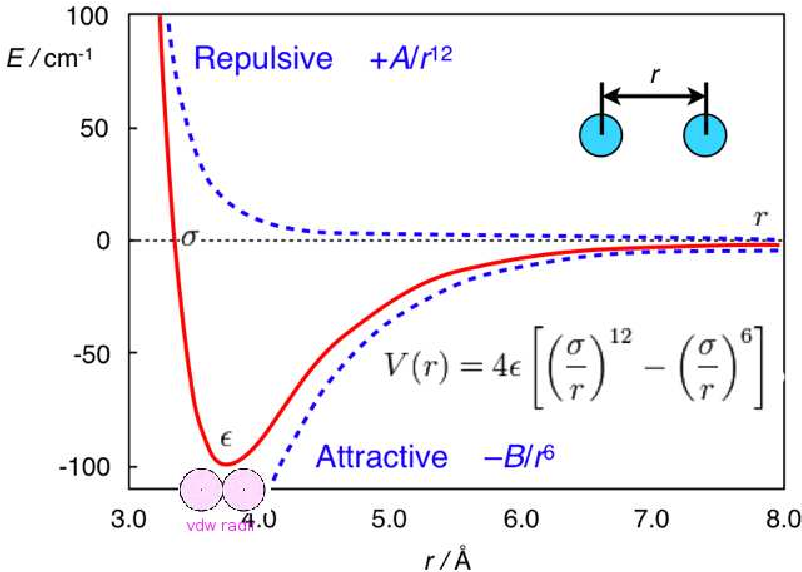
Lennard-Jones potentials are used in the models of vdW interactions.

Lenard Jones potential : The distance between the centers of two particles affects the Lennard-Jones potential. There is very little chance of two non-bonding particles getting together and interacting when they are infinitely far apart. For the purpose of simplicity, their bonding potential energy is taken to be zero.

the Lennard-Jones potential describes the potential energy of interaction between two non-bonding atoms or molecules based on their distance of separation. 

 

The Lennard-Jones model consists of two 'parts' :

•  a steep repulsive term.

• smoother attractive term, representing the London dispersion forces.

The Lennard-Jones potential simulates interactions between softly appealing and repulsively. The Lennard-Jones potential therefore defines electrically neutral atoms or molecules.

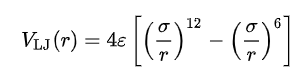
where "sigma" is the distance at which the particle-particle potential energy

'V' is the intermolecular potential between the two atoms or molecules.

'ϵ' is the well depth and a measure of how strongly the two particles attract each other.

'σ' is the distance at which the intermolecular potential between the two particles is zero. σ gives a measurement of how close two nonbonding particles can get and is thus referred to as the van der Waals radius. It is equal to one-half of the internuclear distance between nonbonding particles.

'r' is the distance of separation between both particles (measured from the center of one particle to the center of the other particle).

At a distance of 'r=rm=2^1/6e, when the potential energy has the value 'V=-e' the Lennard-Jones potential is at its smallest.

 

Force fields

The overall MM energy of a molecular system is calculated as the sum of individual energy terms in a force field (FF).

 

Force constants are coefficients (K values) that fit experimental values (such as those from spectroscopy).

 

Potential Energy Surface

The total potential energy is determined as the MM-FF energy for a given molecule or molecular system.

A molecule's potential energy depends on its conformation.

The degrees of freedom (number of rotatable bonds, dihedral angles) in a molecule determine how much conformational space is available.

Calculated potential energy creates an n-dimensional potential energy surface for n degrees of freedom.

Through systematic change of degrees of freedom, conformational search can be used to investigate a molecule's PES.

Each measured set of torsion angles establishes a distinct conformation with a corresponding FF-based potential energy.

Numerous local minima and transition states can be found in the corresponding PES (barriers).

 

Conformational Search

Due to the combinatorial explosion of possible combinations of bond rotations, thorough conformational search is impractical even for tiny molecules (360 degrees per bond)

Consequently, conformational sampling is a heuristic. Each local minimum on the PES defines a family of energetically diverse but closely related conformations.

Sampling and FF energy minimization must work together for conformational exploration to be successful.

 

Energy Minimization

Given an object (atom) with potential energy "Ep," the force acting on the atom is represented by its negative first derivative with regard to position:

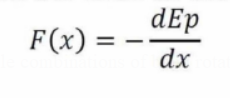
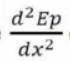
On PES, dEp/dx =0 and d²Ep/dx²>0 and <0 describe a local minimum or local maximum (transition state), respectively

Determine the force F acting on each atom in the given molecule;

Move an atom by a predetermined interval Δx in the direction of the force if it exceeds a predetermined threshold (convergence criterion).

Until convergence is attained, iterate.

A molecule's conformation is altered by EM until it achieves the PES's nearest local minimum.

A family of conformers close to each local minimum is represented by the minimized conformation.

 

EM Algorithms

Popular EM algorithms:
Steepest Descent: st derivative, proteins and small molecules.

Conjugate Gradients: 1st derivative, proteins and small molecules.

Newton-Raphson: 1st and 2nd derivative, small molecules.

Steepest descent This approach is suitable for initial refining of severely strained structures as it is resilient yet slowly converges.

Conjugate gradients: This approach is more effective and makes better decisions regarding the direction of the search. It is appropriate for large system minimization.

Newton-Raphson: This minimizer determines the slope and rate of the energy change associated with conformation. It can be used to achieve extremely high convergence on systems that have already undergone refinement, but it is inefficient for big systems.

Protocol for use in real world situations (small molecules)

The steepest descent takes about 50 iterations, during which the strongest stresses on an atom are removed in order to fix significant structural faults.

Conjugate Gradients: around 100 it. : reduce energy (of great magnitude, optimize geometry, and bring conformations close to the local minimum (shallow gradient)

Newton-Raphson: around 50 it.: reduce energy (by a little amount) and alter minute structural features until the absolute minimum is obtained.

 

Molecular Dynamics

Since EM "moves down slopes," it cannot pass through obstacles or transition states on the PES.

Molecules can penetrate PES barriers using molecular dynamics (MD) simulations.

By repeatedly calculating Newton's equation of motion, MD determines the trajectories of atomic motions.

Newton's equation of motion is for atom i.

F_i-m_ia_i

F_i (t) = m_i d²r_i (t)/dt²

The location and mass of atom I are, respectively, "ri" and "m."

The force on atom I at time step "t" is known as "Fi(t)".

Acceleration ('a') is the second derivative of an atomic position ('r') with respect to time.

The negative first derivative of potential energy at time step "t" can be used to determine "Fi(t)".

The formula calculates the force acting on an atom across time-dependent changes in location.

The equation of motion needs to be integrated over time in order to produce a trajectory of atomic movements.

The next position is determined using the position and acceleration at time step t and the preceding position r(t—𝛿t).

(Verlet algorithm):
r(t + 𝛿t) = 2r(t) — r(t — 𝛿t) + 𝛿t²a(t)

The most rapid atomic motion (10 fs hydrogen vibration) is chosen as a time step 𝛿t, which is commonly 1 fs (10^–15 s).

Simulated Annealing

MD and simulated annealing can be used together to screen a molecular system's PES (SA).

By raising and lowering the system's temperature T and consequently its kinetic energy, SA entails "heating" and "cooling" cycles.

Heating: obstacles are surmounted during mobility.

Local minima are found during cooling.

EM sample conformations in local minima are followed by SA "snapshots" taken during cooling.

 

Energy in Force Fields

Potential energy in MM FF

- Are determined using vacuum.

- Are not relevant to chemistry.

- Have no connection to the Gibbs free energy in thermodynamics.

- Absolute numbers are meaningless.

- Is not comparable amongst molecules.

- Can only be compared relative to other conformers of the same molecule or to compounds that are highly similar (analogs)

 

Energy Minimization

Highly efficient in creating low-energy conformations, optimizing bound and non-bonded interactions, and adjusting molecular geometry

 

 

---- Summary ----

As of now you know all basics of all the laws of thermodynamics.

• Potential Energy Surface

• Energy minimization

• Force fields

• etc..