8. Thermodynamics:

Thermochemistry

A substance change in a chemical reaction is typically accompanied by an energy change.

The energy that is released or absorbed can take on various forms, including heat but also light, electric energy, mechanical energy, and others.

The study of energy change—expressed as heat—associated with chemical changes is known as thermochemistry.

 

Measuring Energy

Newton's second law of motion in classical mechanics gives us the following relationship between a force F and the acceleration a that a body of mass m experiences:

F=ma

In Newtons, force is measured (N).

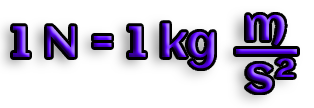
A mass of 1 kg moving at 1 m/s^2 requires a force of 1 Newton:

The dot product of a force F and the work W is referred to as

W=F-d

the displacement of an item by the given distance d.

In Joules, work is measured (J).

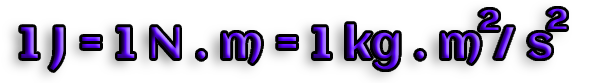
The labor required to apply a force of 1 N over a distance of 1 m is measured in units of joules:

A body of mass m has kinetic energy E_kin if it is accelerated to a velocity of v using the work W.

The kinetic energy is connected to mass and velocity and equivalent to the work W:

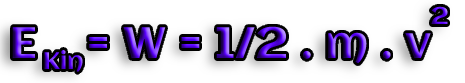
Consequently, the Joule is the unit of kinetic energy (J)

 

Conversation of energy

Energy cannot be created or destroyed in a closed system, but it can be changed from one form to another.

When friction slows a moving object with kinetic energy (Ekin), the kinetic energy is converted to heat until the object comes to rest.

Independent of the specific form it takes, energy is measured in Joules.

 

Heating and Temperature

Every object has the potential to have thermal energy. At T > 0K, the energy is connected to the random motion of molecules.

If two things in thermal contact are at different temperatures, they can exchange energy as heat. The system eventually finds equilibrium, and its macroscopic properties remain unchanged.

In Kelvin [K], temperature is measured.

or in degrees Celsius [°C], where x K = (x - 273.15) °C

 

Heat capacity

Heat capacity C [J/K] : The quantity of heat/energy (1J) required to raise an object's temperature by 1K; [J/K].

Specific Heat Capacity [J/gK] : The amount of energy(1J) required to raise 1g of a substance's temperature by 1K is known as its specific heat (or capacity; unit: [ J/gK ]).

In the past, a heat-based energy unit called the calorie was defined using the specific heat capacity of water.

1 cal = 4.184 J

 

Substances	Phase	Specific heat capacity
Air (Sea level, dry, 0 °C (273.15 K))	gas	1.0035
Air (typical room conditionsA)	gas	1.012
Aluminium	solid	0.897
Ammonia	liquid	4.7
Animal tissue(incl. human)	mixed	3.5
Antimony	solid	0.207
Argon	gas	0.5203
Arsenic	solid	0.328
Beryllium	solid	1.82
Bismuth	solid	0.123
Cadmium	solid	0.231
Carbon dioxide CO2	gas	0.839
Chromium	solid	0.449
Copper	solid	0.385
Diamond	solid	0.5091
Ethanol	liquid	2.44
Gasoline (octane)	liquid	2.22
Glass	solid	0.84
Gold	solid	0.129
Granite	solid	0.79
Graphite	solid	0.71
Helium	gas	5.1932
Hydrogen	gas	14.3
Hydrogen sulfide H2S	gas	1.015B
Iron	solid	0.412
Lead	solid	0.129
Lithium	solid	3.58
Lithium at 181 °C	solid(?)	4.233
Lithium at 181 °C	liquid	4.379
Magnesium	solid	1.02
Mercury	liquid	0.1395
Methane at 2 °C	gas	2.191
Methanol	liquid	2.14
Molten salt (142–540 °C)	liquid	1.56
Nitrogen	gas	1.04
Neon	gas	1.0301
Oxygen	gas	0.918
Paraffin wax C25H52	solid	2.5 (ave)
Polyethylene (rotomolding grade)	solid	2.3027
Silica (fused)	solid	0.703
Silver	solid	0.233
Sodium	solid	1.23
Steel	solid	0.466
Tin	solid	0.227
Titanium	solid	0.523
Tungsten	solid	0.134
Uranium	solid	0.116
Water at 100 °C (steam)	gas	2.08
Water at 25 °C	liquid	4.1813
Water at 100 °C	liquid	4.1813
Water at −10 °C (ice)	solid	2.05
Zinc	solid	0.387

Table 1. List of various substances and their specific heat capacities.

 

Calorimetry

In calorimetry, a calorimeter is used to calculate how much heat is produced or absorbed during a chemical reaction.

>> calorimeter image

 

heat transfer :

 

Example question :

In a calorimeter containing 1.20 kg of water, glucose is oxidized. What amount of heat will be emitted if the temperature rises from 19°C to 25.5°C degrees Celsius ?

Answer :

C_p(H₂O)     =              4.184 kJ . kg^-1.K^-1

C_device        =              2.21 kJ.K^-1

C_water         =               4.184 KJ .kg^-1.K^-1 * 1.20 kg        = 5.02 kJ.K^-1

C_total          =                C_device + C_water                            = 7.23 kJ.K^-1

Final Answer:

      Q         =                 C_total.(T_after-  T_before)                = 7.23kJ.K^-1 .(25.5°C    -   19°C)      =   47 kJ

 

Thermodynamics

The science of energy conversion during physical and chemical processes is known as thermodynamics.

Using thermodynamics to foretell whether reactions would take place spontaneously under specific circumstances is a crucial application in chemistry.

 

Thermodynamic system

A system is viewed as a constrained, clearly defined macroscopic spatial region with specified parameters while studying the principles of thermodynamics.

Different interactions between a system and its environment are possible depending on the nature of the system.

 

Types of system	Mass	Work	Heat
Open	Yes	Yes	Yes
Closed	No	Yes	Yes
Adiabatic	No	Yes	No
Isochoric	No	No	Yes
Isolated	No	No	No

Table 2. Different types of thermodynamic systems.

 

State functions

A thermodynamic systems macroscopic features are quantitatively described by state functions.

Examples:

• Volume

• Pressure

• Temperature

As their name suggests, they are merely reliant on the system's current condition, regardless of the precise course that brought it about.

 

Equation of State

a formula for the relationship between state functions. The ideal gas law is one such and is described below :

p                 :   pressure [Pa = N/m²]

V                :   volume [m³]

n                 :   amount of substance [mol]

R                :   universal gas constant (8.314 J/mol.K)

T                :   absolute temperature [K]

Based on this formula we are able to measure the energy of a system :                    N/m  =>          J      => Energy

 

The 0^th law of thermodynamics

They are in thermal equilibrium with one another if two bodies A and B are in thermal equilibrium with body C.

This law can be used to build thermometers that measure a body's temperature.

 

The 1^st law of thermodynamics

For thermodynamic systems, an energy balance can be obtained using the energy conservation principle.

Consequently, an energetic state function is established, which represents the system's internal energy U.

As a state function, a system's core energy is only influenced by its current state and not by the steps that brought it about.

Consequently, there is a continual difference in the internal energy of two different states.

 

ΔU    =         U₂       -      U₁

 

The first law of thermodynamics states that inner energy has a state function and that any change in inner energy equals the heat absorbed and the work performed by the system.

ΔU    =          Q       -       W

Sign conventions

Q>0    : system take up heat

Q<0    : system releases heat

W>0   : system does work

W<0   : work is done to the system

ΔU>0  : system takes up energy

ΔU<0  : system loses energy

 

Enthalpy is the sum of the system's internal energy and the product of its pressure and volume.

Typically, chemical reactions take place under a constant amount of pressure.

As a result, when a process involves mechanical work, the system expands in opposition to the applied pressure (e.g. if gases are produced)

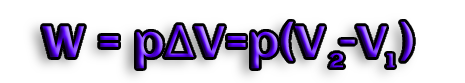
In this instance, we define the enthalpy change ΔH as:

substitution of ΔH for Q in ΔU = Q - W

ΔU = ΔH - W

ΔH=ΔU+W   ; W=pΔV

ΔH=ΔU+pΔV

The enthalpy H is a state function, just like the inner energy U. It's outlined as:

H  =  U  +   pV

Once more, the difference in enthalpies between two states is constant and independent of path:

ΔH  =  H₂  -  H₁

Solids and liquids have extremely minimal volume changes, but if gases are involved in a chemical reaction, their volume could change dramatically.

The change in material amount can be used to compute the difference in volume if pressure and temperature are both constant:

p(V₂-V₁)=(n₂-n₁)RT                   <==>    pΔV   =  ΔnRT

ΔH=ΔU+pΔV

ΔH=ΔU+ΔnRT

therefore we get the final formula :

 

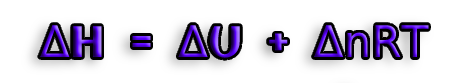
Example question :

The energy emitted by burning CH₄ was calculated in a calorimeter at 25°C under constant volume to be -885.4 kJ/mol.
Calculate the reaction's ΔH.

Answer :

CH₄ (g) + 20₂ (g)     —>      CO₂ (g)   +    2H₂O (l)           ΔU = -885.4 kJ/m0|

n_R= 3 mol               n_P=1

ΔH = ΔU + ΔnRT

=   -885.4 kJ/mol    +    ((  1-3  ).(  8.314-10^-3 kJ/mol.K    -   298.2 K   ))

=   -885.4 kJ/mol - 4.95 kJ/mol

=   -890.4 kJ/mol

 

A reaction is called endothermic if ΔH > 0 and exothermic if ΔH < 0.

 

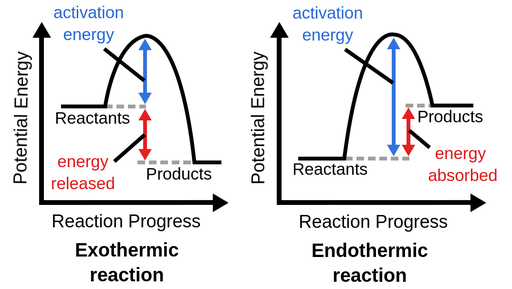
Figure 1. Heat is released during an exothermic reaction, raising the temperature of the immediate environment. An endothermic process removes heat from the environment and cools it.

 

Whether a change occurs in a single step or multiple steps, the enthalpy released or absorbed is the same in each case.

The law of energy conservation and Hess' law are compatible.

 

 

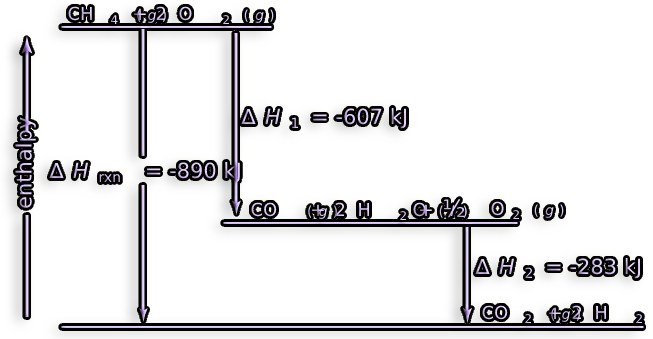
Energy creation would be conceivable if the net change in energy varied depending on the actions conducted, which is not possible.

According to Hess's law, as long as the beginning and final states of the reactants and products are the same, the change in enthalpy in a chemical reaction will be the same whether the reaction occurs in one step or multiple steps.

In other words, regardless of the method through which a chemical change happens, if a chemical change occurs by numerous different routes, the overall enthalpy change will be the same.

Even when it cannot be measured directly, Hess's law enables the calculation of the enthalpy change (H) for a reaction.

net change in enthalpy                          :      ΔH_net

sum change in enthalpy reactions         :      ∑ΔH_r

 

A net or overall equation is created by combining chemical equations.

If the enthalpy changes for every equation in the series are known, the enthalpy change for the net equation will be the total of those values.

The process is exothermic and is more likely to be spontaneous if the net enthalpy change is negative, whereas positive H values are associated with endothermic reactions.

 

Standard Enthalpy of Formation

The values of the standard enthalpy of formation can be used to compute reaction enthalpies.

It is the change in enthalpy that occurs when an element is converted into a 1 mol pure substance from its standard state*

Standard state*  : i.e., the most stable form of the element at 1 bar [or, occasionally, 101.13 kPa] and a specific temperature, typically 25°C)

Symbol is ΔH⁰_f

C(graphite) + O₂(g) —> CO₂(g)                      ΔH⁰_f  :  393.5kJ.mol^-1

Just like this there are several standard enthalpies of formation unique to each substance.

 

Compute Enthalpies

From standard enthalpies of formation, the standard enthalpy of a reaction can be computed as follows:

ΔH°         =         ΔH_f°(products)           -              ΔH_f°(reactants)

 

Hydrogenation of ethene :

C₂H₄(g) + H₂(g) —> C₂H₆(g)

2C(graphite) + 2H₂(g)                  —>                       C₂H₄(g)                           ΔHf°   =      52.30 kJ/mol

2C(graphite) + 3H₂(g)                  —>                       C₂H₆(g)                          ΔHf°    =      -84.68 kJ/mol

C₂H₄(9) + H₂(g)                           —>                     C₂H₆(g)                            ΔH°     =      -136.98 kJ/mol

 

Energy lattices and the Born-Haber Cycle

Keep in mind that ions create crystals. It is impossible to directly measure the energy released when creating a crystal from ions in the gas phase.

Figure 2. The lattice energy of NaCl is 787.3 kJ/mol, which is just somewhat less than the energy released during the combustion of natural gas. When the ions are tiny, the binding between ions with opposite charges is strongest.

 

It can be computed from other empirically determined values using Hess' law.

The Born-Haber cycle is the name of this approach.

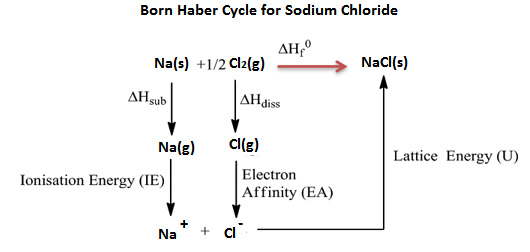
Figure 2. The born haber cycle for NaCl.

 

A Born Haber cycle is a series of enthalpy changes that results in the production of a solid, crystalline ionic compound from elemental atoms in their standard state, with the net enthalpy of the solid compound decreasing to zero.

 

Born Haber cycle for NaCl:

Step 1: Sublimation of metallic sodium of gaseous sodium atom with the enthalpy of sublimation = △H_s

Na(s)→Na(g);△H=△H_s

 

Step 2 : Dissociation of molecule of chlorine to chlorine atoms with enthalpy of dissociation = △H_d

 1/2Cl₂(g)→Cl(g);△H=△H

 

Step 3: Ionization of gaseous sodium with the enthalpy of ionization = △H_i

Na(g)→Na⁺ (g)

 

Step 4: Addition of electron to gaseous chlorine atom with the enthalpy of electron affinity = △HEa

Cl (g) +e⁻→Cl⁻(g),△H=△HEa

 

Step 5: Close packing of gaseous sodium ion and chloride ion to form the lattice structure of NaCl, with lattice chloride ion to form a lattice structure of NaCl with Lattice energy = U.

NaCl⁺(g)+Cl⁻(g)→NaCl△;△H=U

Step 6: But the sum of all the energies will be equal to the heat of formation of one mole of sodium chloride from its reluctant i.e, △Hf

Na(s)+1/2Cl₂ (g)→NaCl(s);△H=△H_f

 

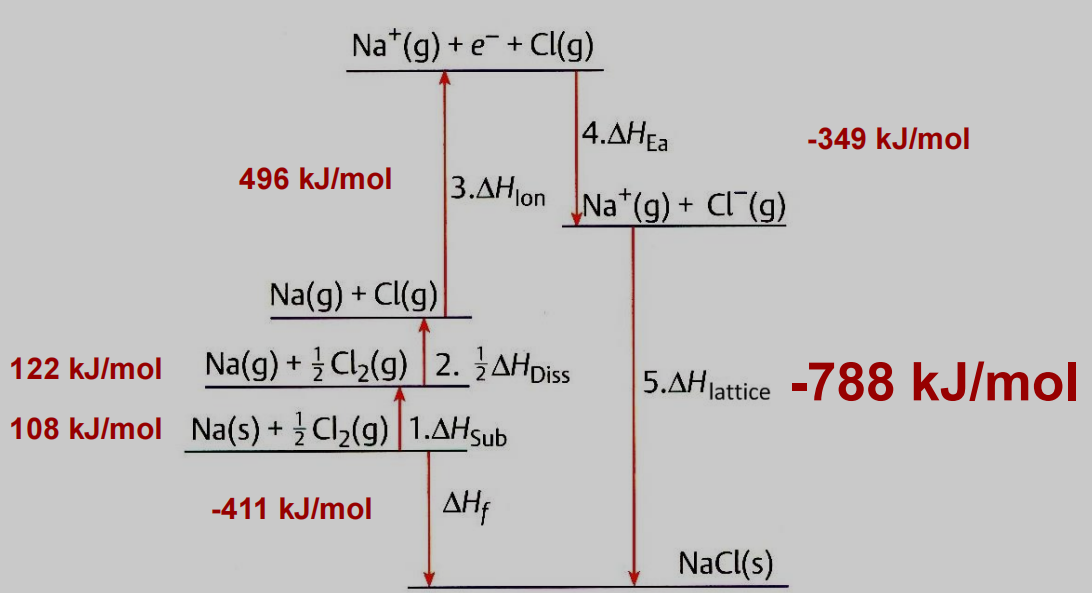
Figure 3. The overall born haber cycle for NaCl.

 

2^nd Law of Thermodynamics

Energy must be conserved during chemical and physical processes, according to the first law.

The second law of thermodynamics asserts that heat cannot move from a reservoir of lower temperature to a reservoir of higher temperature in a cyclic process.

Even yet, we are unsure of which processes will be triggered spontaneously and which won't.

The entropy S, a new state function introduced by the second law of thermodynamics, allows us to predict whether a reaction will be spontaneous or not.

 

Entropy

One way to think of a system's entropy is as a measure of its disorder; the higher the entropy, the lesser the system's order.

Figure 4. The overall entropy os a sysytem is linked to the order and disorder of the system.

 

Entropy will rise in a spontaneous (naturally occurring) process.

The highest order and least entropy are found in the solid, crystalline state of a given substance. The liquid state has an intermediate entropy, and the gas state has the maximum entropy.

Melting and vaporization: entropy increases

Condensation and freezing: entropy reduction

 

Things shouldn't spontaneously condense or freeze if we say the second law would only apply to a specific system.

As a result, we also need to take the environment's and the system's entropy changes into account:

ΔS_tot    =    ΔS_sys  +   ΔS_env

 

Energy is released (negative enthalpy) when a liquid freezes and is absorbed by the surroundings. This makes the environment more entropic.

Always take into account the overall change in entropy.

Heat emitted by the system is what causes the environment's entropy to alter.

The environment's change in entropy for a process occurring at constant pressure and temperature can be computed as follows:

entropy units are :  J/K

 

Gibbs Free energy

ΔS_env  =  ΔH/T

ΔS_env = ΔS_tot +ΔS_sys

ΔS_tot +ΔS_sys = ΔH/T

TΔS_tot  + TΔS_sys  =ΔH

Substitute ΔG for -TΔS_tot  :   

ΔG  + TΔS_sys=  ΔH

ΔG  =  ΔH-TΔS_sys

ΔG  =  ΔH-TΔS    changes in gibbs free energy

G  =  H-TS            gibbs free energy

 

Meaning of ΔG  :

G is like H and S- a state function     ΔG  =  G₂-G₁

Finally, the Gibbs free energy function allows us to determine whether a process will occur spontaneously under specific conditions (temperature and pressure constant)

ΔG > 0  reaction will not happen spontaneously.

ΔG = 0 System is in thermodynamic equilibrium.

ΔG < 0 reaction will happen spontaneously.

 

Figure 5. Some reactions with respect to gibbs free energy.

 

Standard Gibbs Energy of Formation

Gibbs free energy change that occurs when 1 mole of a substance is formed from its constituent elements in their standard states (often at 1 bar and 25°C).

 

3rd Law of Thermodynamics

As the absolute temperature gets closer to zero, the entropy of a perfect crystal decreases.

The third law of thermodynamics states that the entropy of a system approaches a constant value as the temperature approaches absolute zero.

The entropy of one mole of substance at standard conditions (often 1 bar/25°C) is known as the standard molar entropy S⁰.

For a reaction, the modification of the standard molar entropy is referred to as ΔS⁰.

 

Example question :

Vaporization of methanol — calculate the normal boiling point of methanol.

H₃COH_(I) <==> H₃COH_(g)

ΔH⁰ = 37.4 kJ/mol

ΔS⁰ = 111 J/(mol.K)

 

The related temperature for "ΔG = 0" is the same as methanol's typical boiling point. We consider "ΔH" and "ΔS" to be temperature-independent.

ΔG⁰  =  ΔH⁰-TΔS⁰ = 0

37.4 kJ/mol - T . 0.111 kJ/(mol-K) = 0

T = (37.4 kJ/mol) / (0.111 kJ/(mol.K) ) = 337 K (64°c)

 

Equilibrium and Free Energy

Fundamentals: Equilibrium must be reached for any thermodynamic system.

If they reduce the Gibbs free energy, the system changes.

The Gibbs free energy is lowered by an increase in entropy and a decrease in enthalpy.

 

---- Summary ----

As of now you know all basics of all the laws of thermodynamics.

• 1st law of thermodynamics

• 2nd law of thermodynamics

• 3rd law of thermodynamics

• etc..